Sådan beregnes en Z-score ved hjælp af Microsoft Excel

En Z-Score er en statistisk værdi, der fortæller dig, hvor mange standardafvigelser en bestemt værdi kommer fra middelværdien af hele datasættet. Du kan bruge AVERAGE- og STDEV.S- eller STDEV.P-formler til at beregne middel- og standardafvigelsen af dine data og derefter bruge disse resultater til at bestemme Z-score for hver værdi.

Hvad er en Z-score, og hvad gør funktionerne AVERAGE, STDEV.S og STDEV.P?

En Z-score er en enkel måde at sammenligne værdier fra to forskellige datasæt. Det defineres som antallet af standardafvigelser væk fra det gennemsnitlige datapunkt ligger. Den generelle formel ser sådan ud:

= (DataPoint-AVERAGE (datasæt)) / STDEV (datasæt)

Her er et eksempel for at hjælpe med at præcisere. Sig, at du ønskede at sammenligne testresultaterne fra to algebra-studerende undervist af forskellige lærere. Du ved, at den første studerende fik 95% på slutprøven i en klasse, og den studerende i den anden klasse scorede 87%.

Ved første øjekast er 95% -graden mere imponerende, men hvad nu hvis læreren i anden klasse gav en vanskeligere eksamen? Du kunne beregne Z-score for hver elevs score baseret på gennemsnittet i hver klasse og standardafvigelsen af scorerne i hver klasse. Sammenligning af de to elevers Z-score kunne afsløre, at den studerende med 87% scoren gjorde sig bedre i forhold til resten af deres klasse end den studerende med 98% scoren gjorde i forhold til resten af deres klasse.

Den første statistiske værdi, du har brug for, er 'middel' og Excel's "AVERAGE" -funktion beregner den værdi. Det tilføjer blot alle værdierne i et celleinterval og deler den summen med antallet af celler, der indeholder numeriske værdier (det ignorerer tomme celler).

Den anden statistiske værdi, vi har brug for, er 'standardafvigelsen', og Excel har to forskellige funktioner til beregning af standardafvigelsen på lidt forskellige måder.

Tidligere versioner af Excel havde kun "STDEV" -funktionen, som beregner standardafvigelsen, mens data behandles som en "prøve" af en population. Excel 2010 brød det i to funktioner, der beregner standardafvigelsen:

STDEV.S: Denne funktion er identisk med den tidligere "STDEV" funktion. Det beregner standardafvigelsen, mens data behandles som en "prøve" af en population. En stikprøve af en befolkning kan være noget som de specielle mygder, der er indsamlet til et forskningsprojekt eller biler, der blev sat til side og brugt til kollisionssikkerhedstestning.
STDEV.P: Denne funktion beregner standardafvigelsen, mens data behandles som hele befolkningen. En hel befolkning ville være noget som alle myg på Jorden eller hver bil i en produktionskørsel af en bestemt model.

Hvilket du vælger er baseret på dit datasæt. Forskellen vil normalt være lille, men resultatet af "STDEV.P" -funktionen vil altid være mindre end resultatet af "STDEV.S" -funktionen for det samme datasæt. Det er en mere konservativ tilgang til at antage, at der er mere variabilitet i dataene.

Lad os se på et eksempel

For vores eksempel har vi to kolonner ("Værdier" og "Z-Score") og tre "hjælper" -celler til opbevaring af resultaterne af funktionerne "AVERAGE", "STDEV.S" og "STDEV.P". Kolonnen "Værdier" indeholder ti tilfældige tal centreret omkring 500, og kolonnen "Z-Score" er hvor vi beregner Z-score ved hjælp af de resultater, der er gemt i 'hjælper'-cellerne.

For det første beregner vi middelværdien af værdierne ved hjælp af funktionen "AVERAGE". Vælg den celle, hvor du vil gemme resultatet af funktionen "AVERAGE".

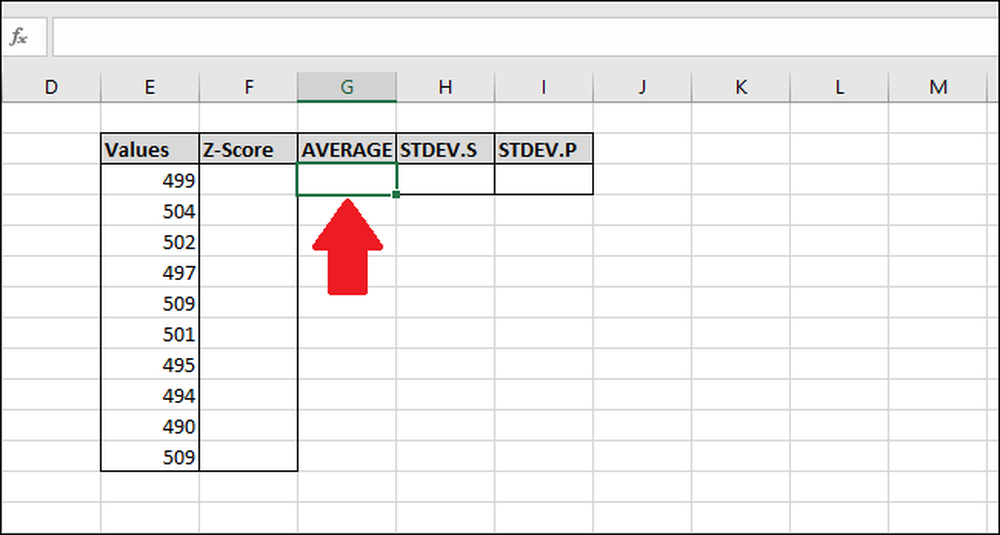
Indtast følgende formel og tryk på gå ind -eller brug menuen "Formler".

= MIDDEL (E2: E13)

For at få adgang til funktionen via menuen "Formler", vælg rullemenuen "Flere funktioner", vælg "Statistisk" og klik derefter på "AVERAGE".

I vinduet Funktionsargumenter markerer du alle cellerne i kolonnen "Værdier" som input for feltet "Nummer1". Du behøver ikke bekymre dig om feltet "Number2".

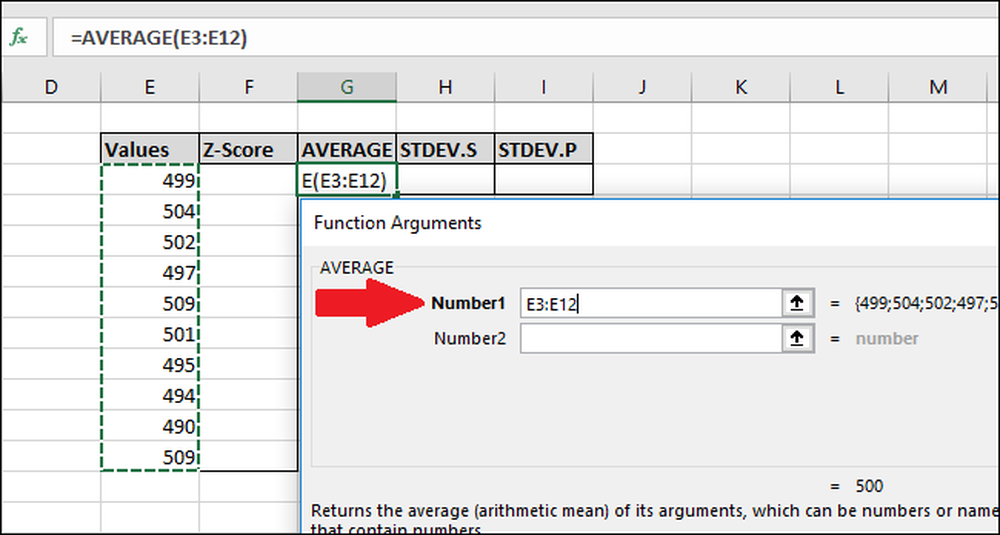
Tryk nu på "OK".

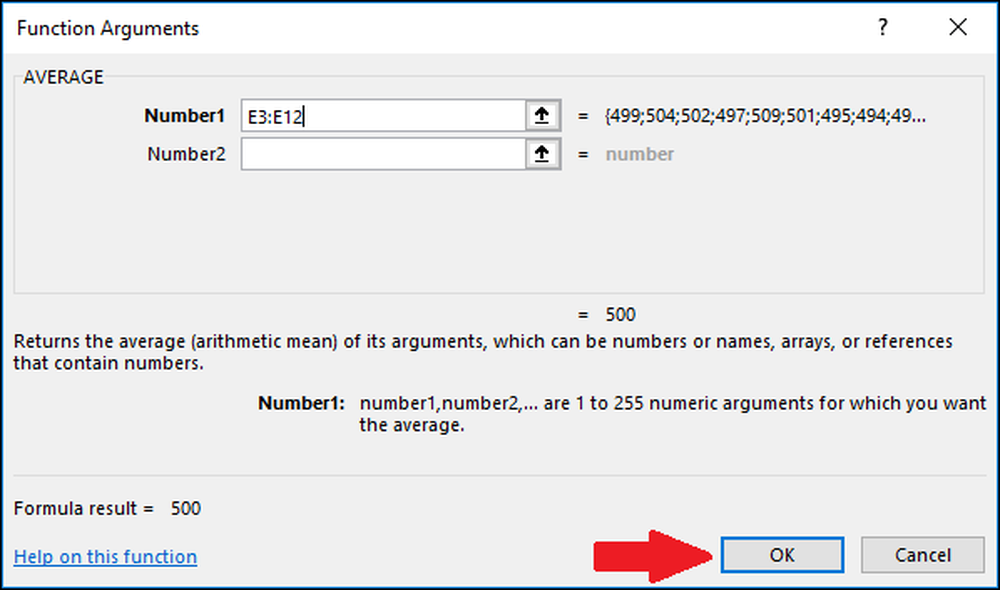
Dernæst skal vi beregne standardafvigelsen for værdierne ved hjælp af enten "STDEV.S" eller "STDEV.P" -funktionen. I dette eksempel vil vi vise dig, hvordan du beregner begge værdier, begyndende med "STDEV.S." Vælg den celle hvor resultatet bliver gemt.

For at beregne standardafvigelsen ved hjælp af funktionen "STDEV.S", skriv denne formel og tryk Enter (eller få adgang til den via menuen "Formler").

= STDEV.S (E3: E12)

For at få adgang til funktionen via menuen "Formler", vælg rullemenuen "Flere funktioner", vælg "Statistisk", rul ned lidt, og klik derefter på kommandoen "STDEV.S".

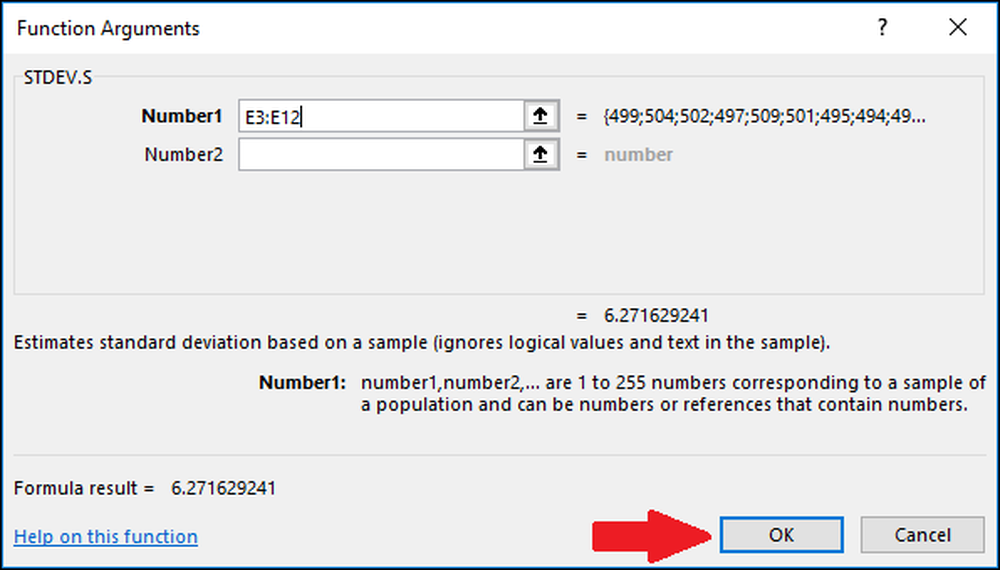
I vinduet Funktionsargumenter markerer du alle cellerne i kolonnen "Værdier" som input for feltet "Nummer1". Du behøver heller ikke bekymre dig om feltet "Number2" her.

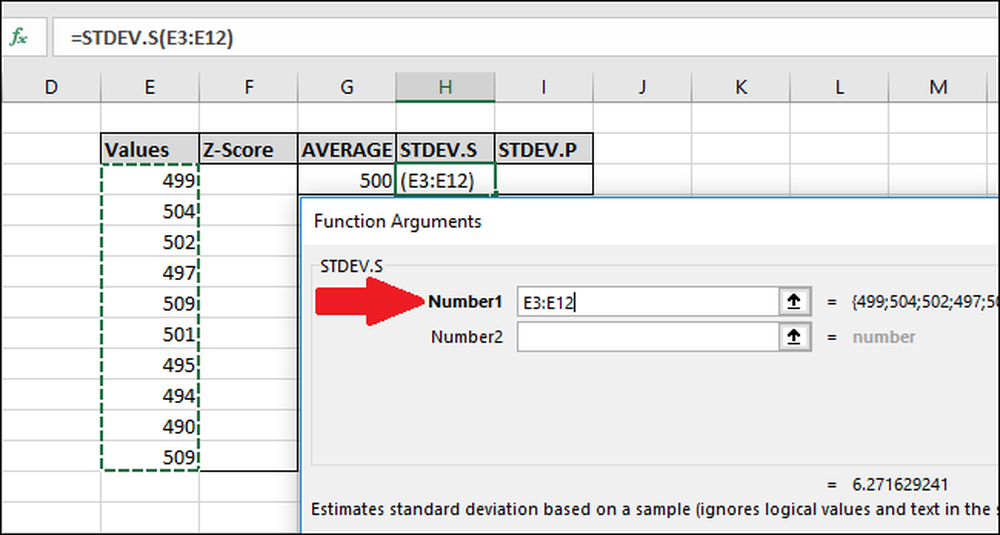
Tryk nu på "OK".

Derefter beregner vi standardafvigelsen ved hjælp af funktionen "STDEV.P". Vælg den celle, hvor resultatet bliver gemt.

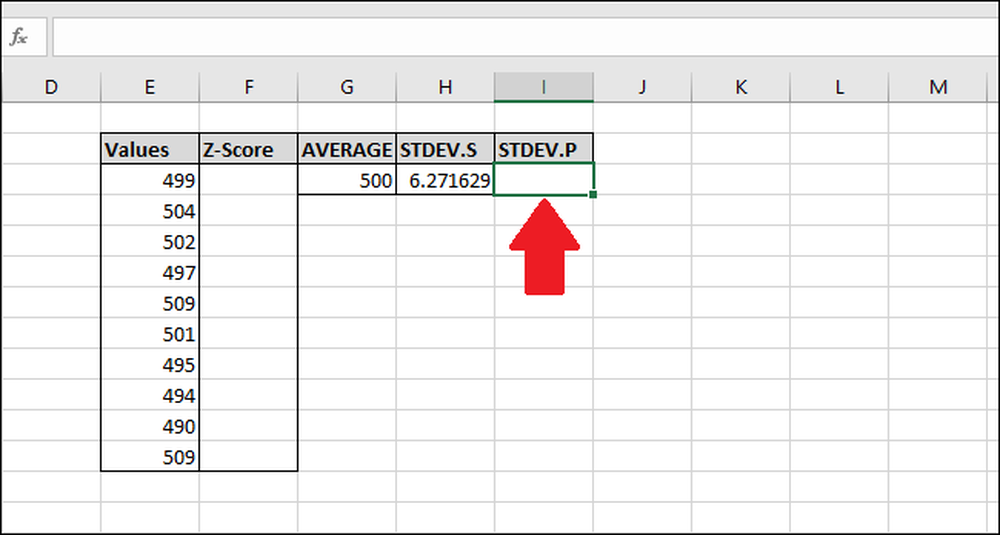
For at beregne standardafvigelsen ved hjælp af funktionen "STDEV.P", skriv denne formel og tryk Enter (eller få adgang til den via menuen "Formler").

= STDEV.P (E3: E12)

For at få adgang til funktionen via menuen "Formler", vælg rullemenuen "Flere funktioner", vælg "Statistisk", rul ned lidt, og klik derefter på "STDEV.P" -formlen.

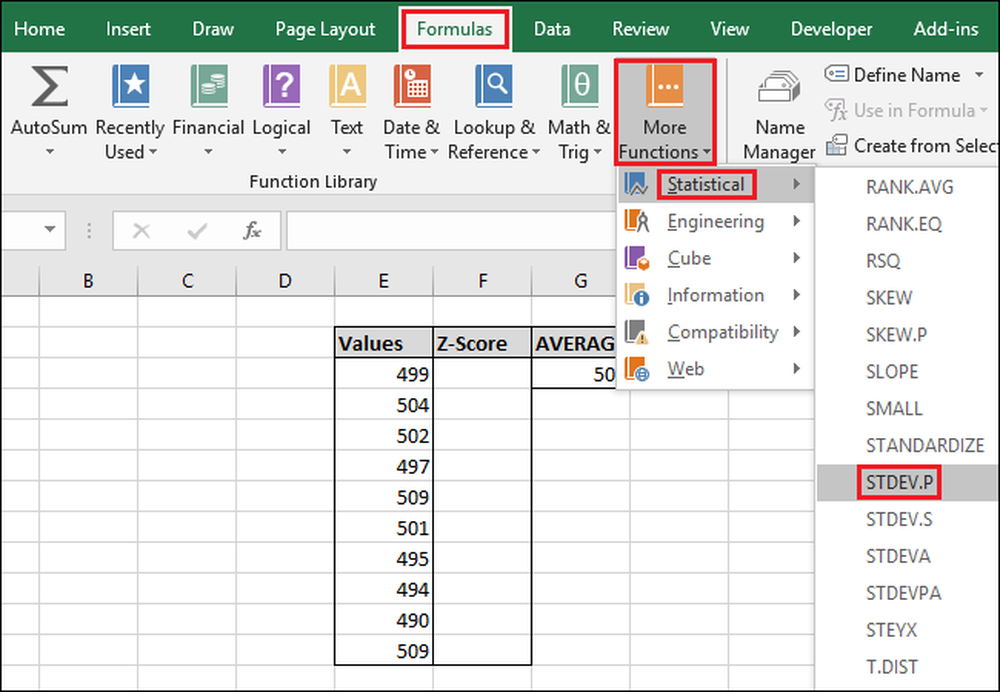
I vinduet Funktionsargumenter markerer du alle cellerne i kolonnen "Værdier" som input for feltet "Nummer1". Igen skal du ikke bekymre dig om feltet "Number2".

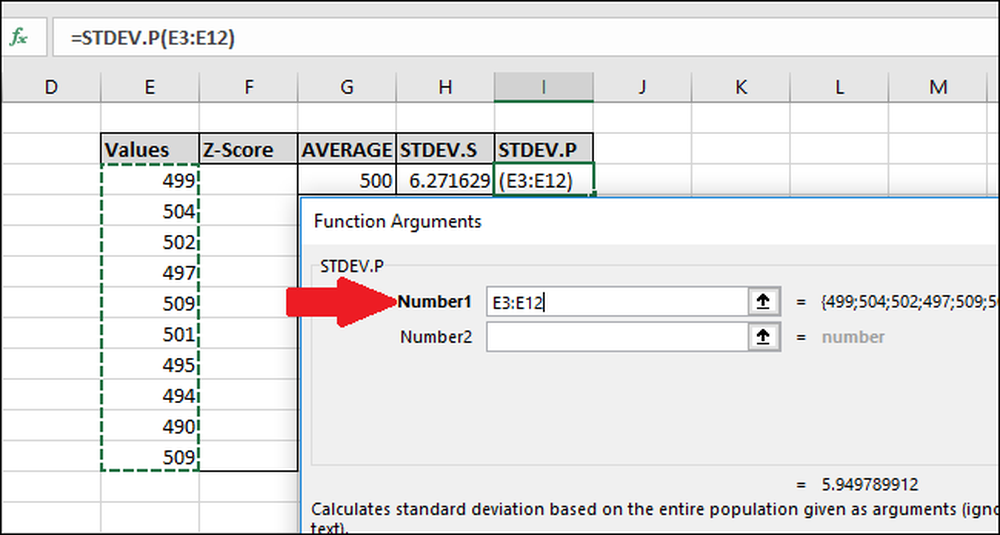
Tryk nu på "OK".

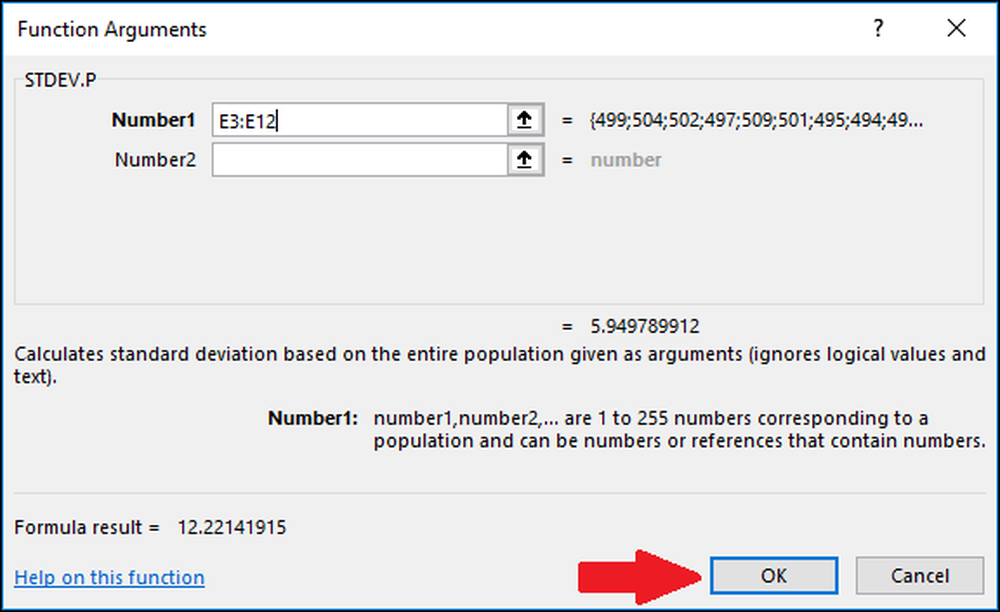
Nu hvor vi har beregnet middel- og standardafvigelsen af vores data, har vi alt, hvad vi har brug for til at beregne Z-score. Vi kan bruge en simpel formel, der refererer til cellerne, der indeholder resultaterne af funktionerne "AVERAGE" og "STDEV.S" eller "STDEV.P"..

Vælg den første celle i kolonnen "Z-Score". Vi vil bruge resultatet af "STDEV.S" -funktionen til dette eksempel, men du kan også bruge resultatet fra "STDEV.P."

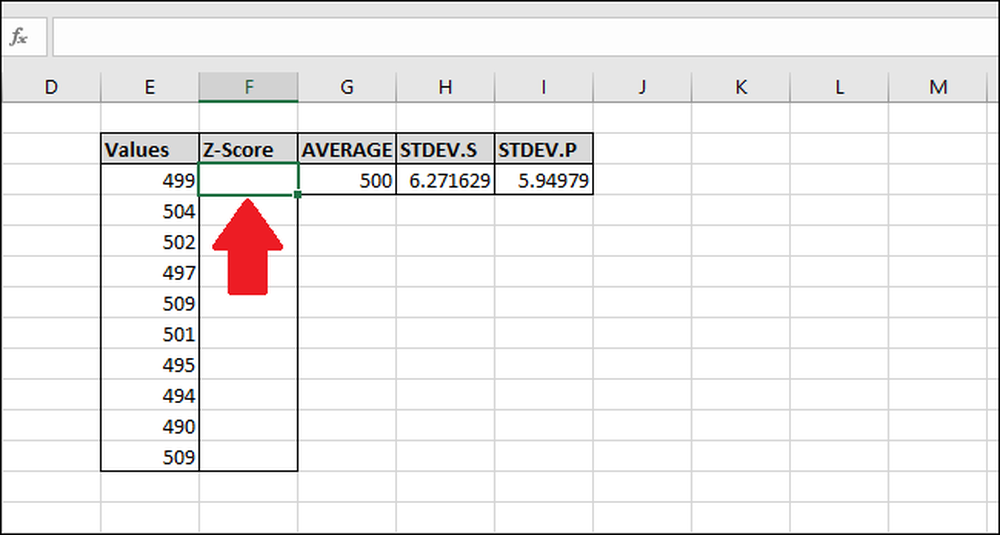
Indtast følgende formel og tryk Enter:

= (E3- $ G $ 3) / $ H $ 3

Alternativt kan du bruge følgende trin til at indtaste formlen i stedet for at skrive:

Klik på celle F3 og skriv = (
Vælg celle E3. (Du kan trykke på venstre-pil-tast en gang eller brug musen)
Indtast minustegnet -
Vælg celle G3 og tryk derefter på F4 at tilføje "$" tegnene for at lave en "absolut" reference til cellen (den vil cykle gennem "G3"> "$G$3 ">" G$3 ">"$G3 ">" G3 ", hvis du fortsætter med at trykke F4)
Type ) /
Vælg celle H3 (eller I3 hvis du bruger "STDEV.P") og tryk på F4 at tilføje de to "$" tegn.
Tryk på Enter

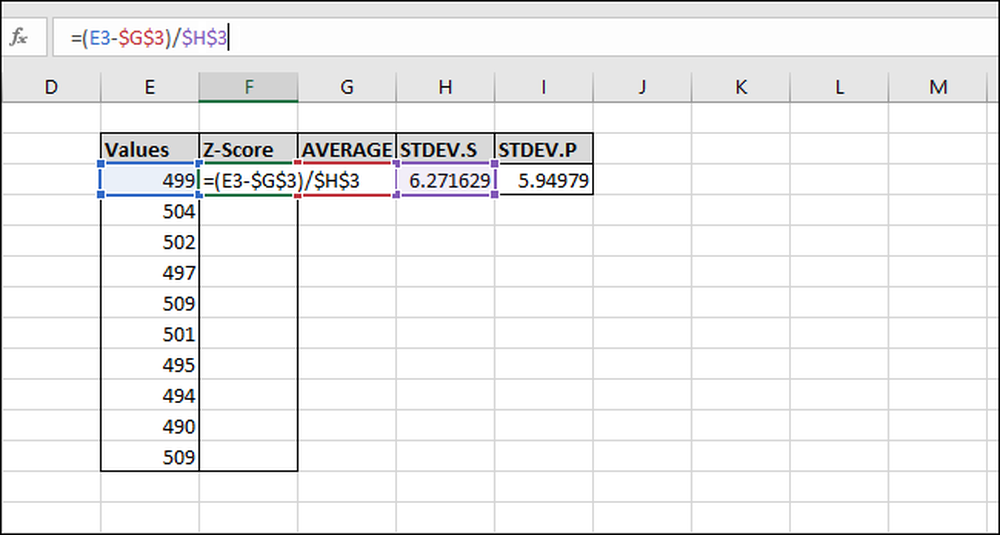
Z-score er beregnet for den første værdi. Det er 0,15945 standardafvigelser under gennemsnittet. For at kontrollere resultaterne kan du multiplicere standardafvigelsen ved dette resultat (6.271629 * -0.15945) og kontrollere, at resultatet er lig med forskellen mellem værdien og middelværdien (499-500). Begge resultater er ens, så værdien giver mening.

Lad os beregne Z-Scores af resten af værdierne. Fremhæv hele kolonnen 'Z-Score', begyndende med cellen indeholdende formlen.

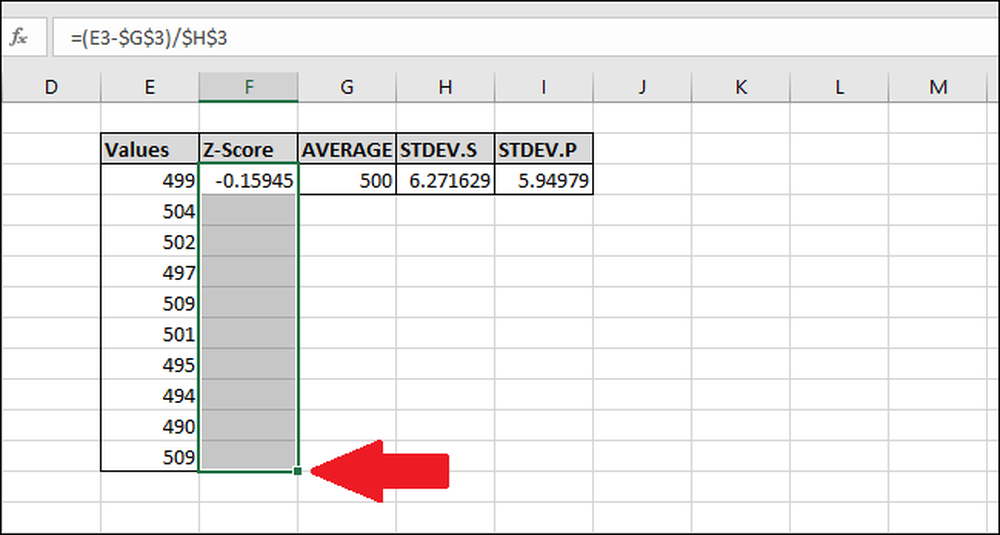
Tryk på Ctrl + D, som kopierer formlen i den øverste celle ned gennem alle de andre valgte celler.

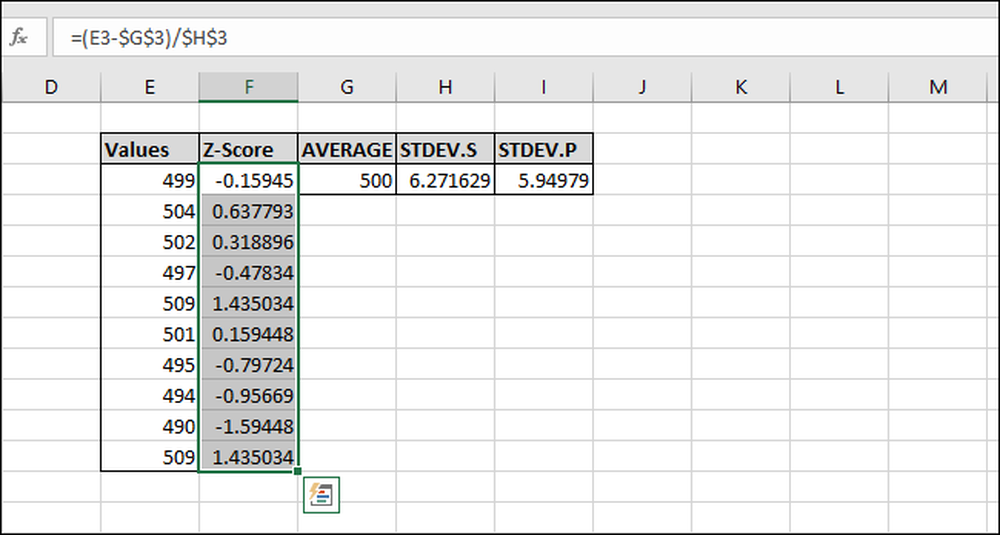
Nu er formlen blevet "fyldt ned" til alle cellerne, og hver vil altid referere til de korrekte "AVERAGE" og "STDEV.S" eller "STDEV.P" celler på grund af "$" tegnene. Hvis du får fejl, skal du gå tilbage og sørg for, at "$" -tegnene er inkluderet i den formel, du indtastede.

Beregning af Z-score uden brug af 'hjælper' celler

Hjælpeceller gemmer et resultat, som dem, der lagrer resultaterne af funktionerne "AVERAGE", "STDEV.S" og "STDEV.P". De kan være nyttige, men er ikke altid nødvendige. Du kan slette dem helt, når du beregner en Z-score ved at bruge følgende generelle formler, i stedet.

Her er en der bruger funktionen "STDEV.S":

= (Value-MIDDEL (Værdier)) / STDEV.S (Værdier)

Og en bruger funktionen "STEV.P":

= (Value-MIDDEL (Værdier)) / STDEV.P (Værdier)

Når du indtaster celleintervallerne for "Værdierne" i funktionerne, skal du sørge for at tilføje absolutte referencer ("$" ved hjælp af F4), så når du 'fill-down' beregner du ikke gennemsnittet eller standardafvigelsen i et andet interval af celler i hver formel.

Hvis du har et stort datasæt, kan det være mere effektivt at bruge hjælperceller, fordi det ikke beregner resultatet af funktionerne "AVERAGE" og "STDEV.S" eller "STDEV.P" hver gang, der sparer processorressourcer og fremskynde den tid det tager at beregne resultaterne.

Også "$ G $ 3" tager færre byte at gemme og mindre RAM for at indlæse end "AVERAGE ($ E $ 3: $ E $ 12).". Dette er vigtigt, fordi standard 32-bit version af Excel er begrænset til 2 GB RAM (64-bit versionen har ingen begrænsninger på, hvor meget RAM der kan bruges).