Opslag, diagrammer, statistikker og drejeborde

Efter at have gennemgået basisfunktioner, cellehenvisninger og dato- og tidsfunktioner, dykker vi nu ind i nogle af de mere avancerede funktioner i Microsoft Excel. Vi præsenterer metoder til at løse klassiske problemer i økonomi, salgsrapporter, fragtomkostninger og statistikker.
SCHOOL NAVIGATION- Hvorfor har du brug for formler og funktioner?
- Definere og oprette en formel
- Relativ og Absolut Cell Reference og Formatering
- Nyttige funktioner, du bør lære at vide
- Opslag, diagrammer, statistikker og drejeborde
Disse funktioner er vigtige for virksomheder, studerende og dem, der bare ønsker at lære mere.
VLOOKUP og HLOOKUP
Her er et eksempel for at illustrere vertikale opslag (VLOOKUP) og horisontale opslag (HLOOKUP) funktioner. Disse funktioner bruges til at oversætte et tal eller en anden værdi til noget, der er forståeligt. For eksempel kan du bruge VLOOKUP til at tage et artikelnummer og returnere varebeskrivelsen.
For at undersøge dette, lad os gå tilbage til vores "Decision Maker" regneark i del 4, hvor Jane forsøger at bestemme, hvad man skal bære i skole. Hun er ikke længere interesseret i, hvad hun bærer, da hun har landet en ny kæreste, så hun vil nu have tilfældige tøj og sko.
I Janes regneark lister hun på tøj i lodrette kolonner og sko, vandrette søjler.
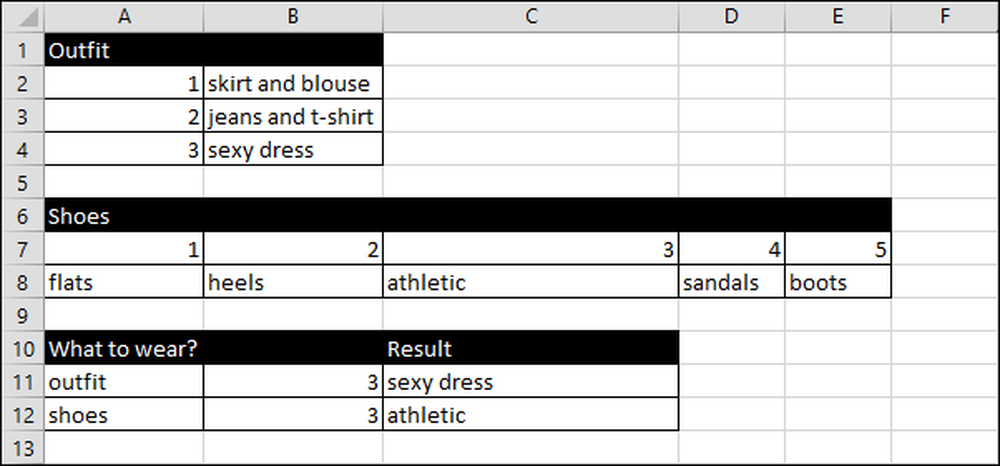
Hun åbner regnearket, og funktionen RANDBETWEEN (1,3) genererer et tal mellem eller lig med en og tre svarende til de tre typer af tøj, hun kan bære.
Hun bruger funktionen RANDBETWEEN (1,5) til at vælge mellem fem typer sko.
Da Jane ikke kan bære et tal, skal vi konvertere dette til et navn, så vi bruger opslagsfunktioner.
Vi bruger VLOOKUP funktionen til at oversætte outfit nummer til outfit navn. HLOOKUP oversætter fra sko nummer til de forskellige typer sko i rækken.
Regnearket virker som dette for outfits:

Excel vælger et tilfældigt tal fra en til tre, da hun har tre outfit muligheder.
Derefter oversætter formlen tallet til tekst ved hjælp af = VLOOKUP (B11, A2: B4,2), der bruger tilfældigt tal værdien fra B11 til at se i intervallet A2: B4. Det giver derefter resultatet (C11) fra de data, der er anført i anden kolonne.
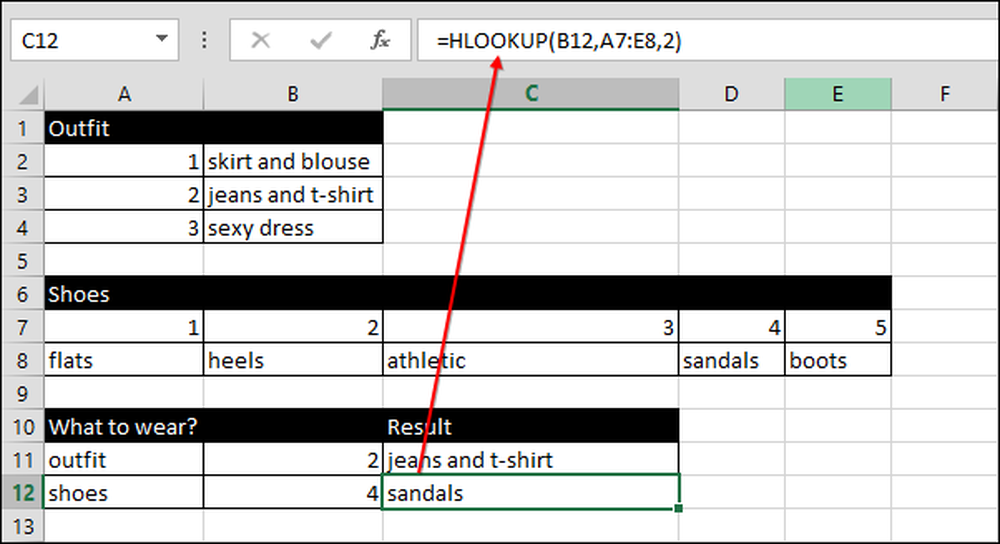
Vi bruger den samme teknik til at vælge sko, undtagen denne gang bruger vi VOOKUP i stedet for HLOOKUP.
Eksempel: Grundlæggende statistik
Næsten alle kender en formel fra statistik - gennemsnitlig - men der er en anden statistik, der er vigtig for erhvervslivet: standardafvigelse.
For eksempel har mange en person, der er gået på college, forværret over deres SAT score. De vil måske gerne vide, hvordan de står i forhold til andre studerende. Universiteterne vil også gerne vide det, fordi mange universiteter, især prestigefyldte, nedviser studerende med lave SAT-scoringer.
Så hvordan skal vi eller et universitet måle og fortolke SAT-score? Nedenfor er SAT-scoringer for fem studerende fra 1.870 til 2.230.
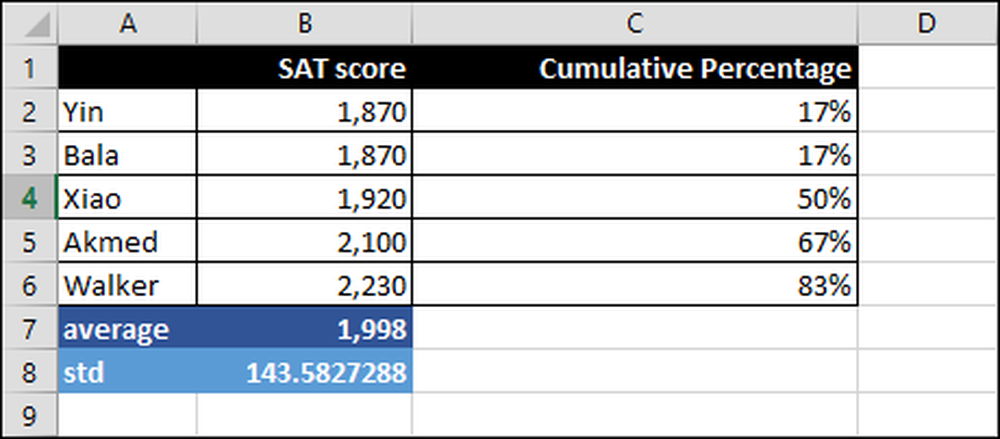
De vigtige tal at forstå er:
Gennemsnit - Gennemsnit er også omtalt som "middel".
Standardafvigelse (STD eller σ) - Dette tal viser, hvor bredt spredt et sæt tal er. Hvis standardafvigelsen er stor, er tallene langt fra hinanden, og hvis det er nul, er alle tal ens. Du kan sige, at standardafvigelsen er den gennemsnitlige forskel mellem gennemsnitsværdien og den observerede værdi, dvs. 1.998 og hver SAT-score. Bemærk, det er almindeligt at forkorte standardafvigelsen ved hjælp af det græske symbol sigma "σ."
Percentiel Rank - Når en elev får en high score, kan de prale med, at de er i top 99 percentilen eller sådan noget. "Percentil rang" betyder procentdelen af scoringer er lavere end en bestemt score.
Standardafvigelse og sandsynlighed er tæt forbundet. Du kan sige, at for hver standardafvigelse er sandsynligheden eller sandsynligheden for, at tallet er inde i det antal standardafvigelser,:
| STD | Andel af scoringer | Udvalg af SAT-scoringer |
| 1 | 68% | 1,854-2,142 |
| 2 | 95% | 1,711-2,285 |
| 3 | 99,73% | 1,567-2,429 |
| 4 | 99,994% | 1,424-2,572 |
Som du kan se, er chancen for, at en SAT-score er udenfor 3 STD'er næsten nul, fordi 99,73 procent af scorerne ligger inden for 3 STD'er.
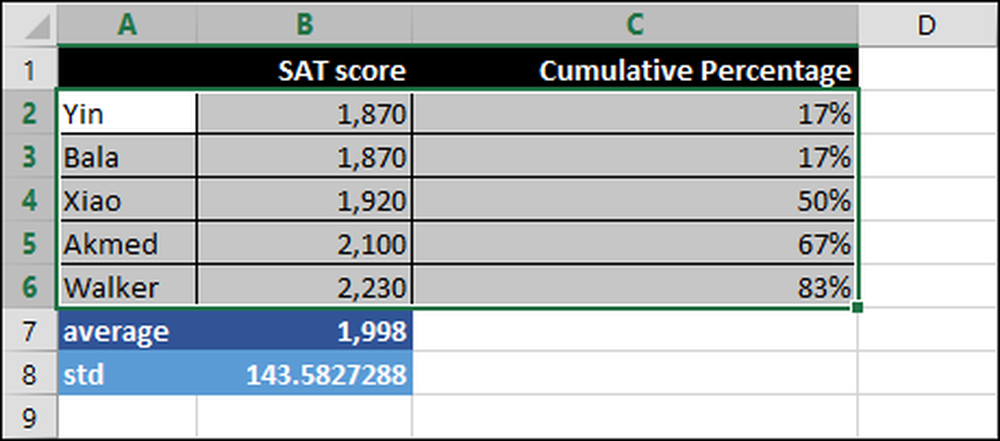
Lad os nu se på regnearket igen og forklare, hvordan det virker.
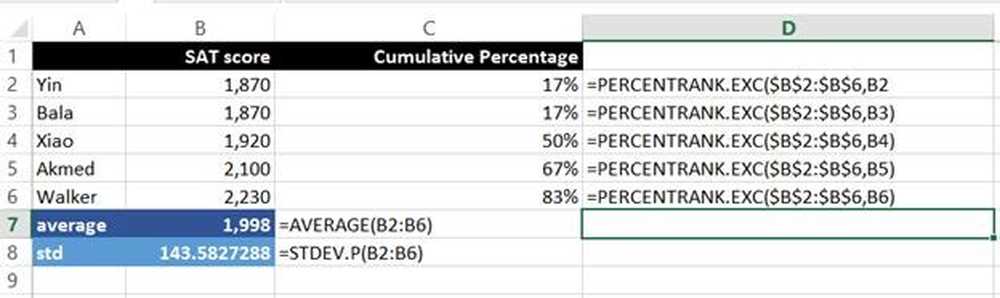
Nu forklarer vi formlerne:
= MIDDEL (B2: B6)
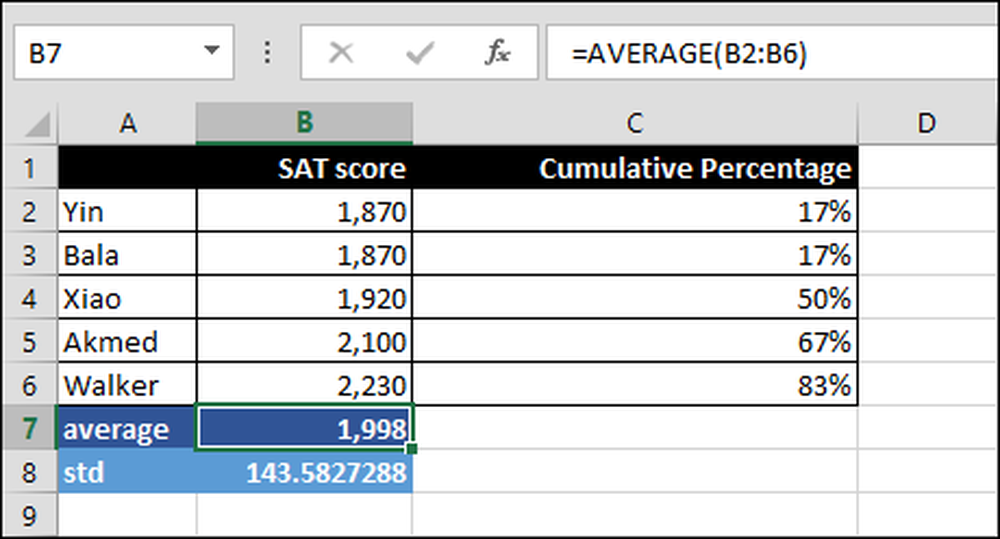
Gennemsnittet af alle scorerne over intervallet B2: B6. Specifikt summen af alle scoringer divideret med antallet af personer, der tog testen.
= STDEV.P (B2: B6)
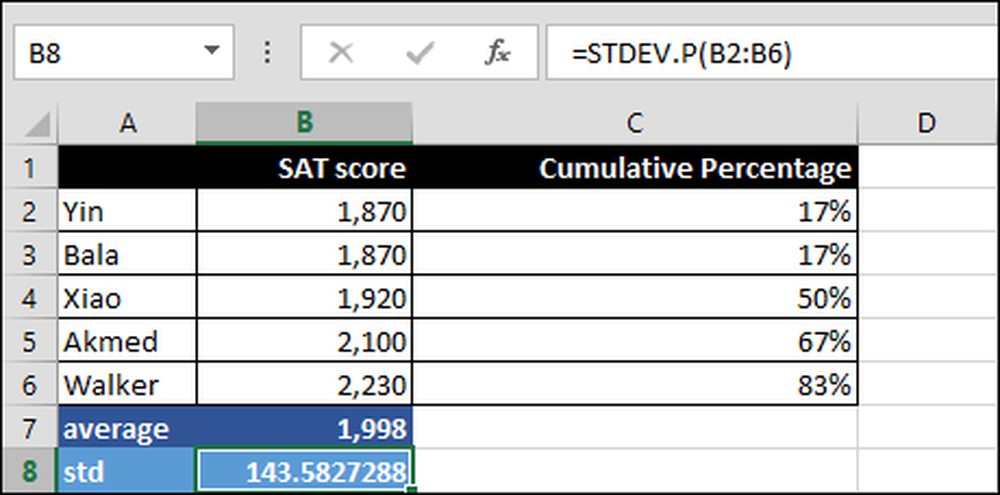
Standardafvigelsen over intervallet B2: B6. ".P" betyder STDEV.P anvendes over alle scorerne, dvs. hele befolkningen og ikke kun en delmængde.
= PERCENTRANK.EXC ($ B $ 2: $ B $ 6, B2)
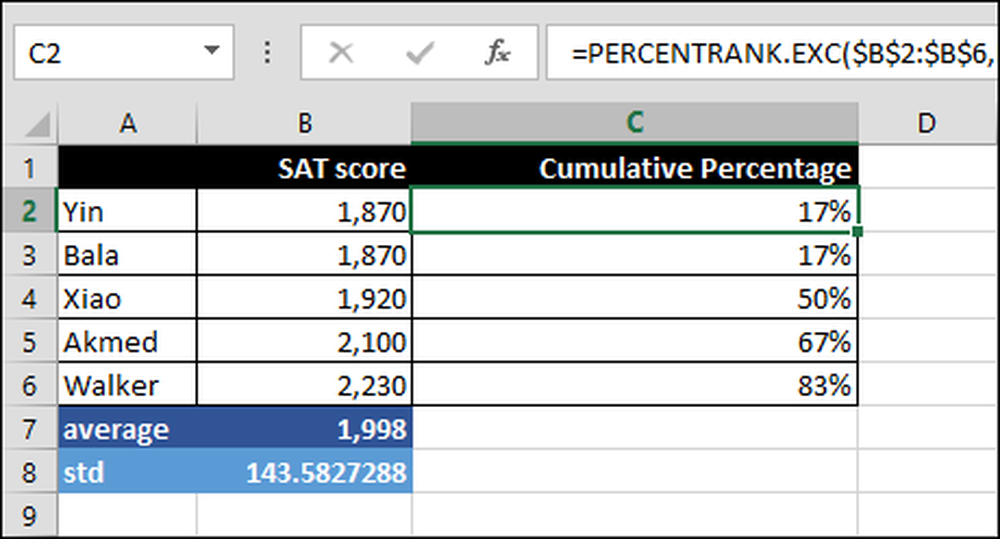
Dette beregner den kumulative procentdel over området B2: B6 baseret på SAT score, i dette tilfælde B2. For eksempel er 83 procent af scorerne under Walker's score.
Grafering af resultaterne
At sætte resultaterne i en graf gør det lettere at forstå resultaterne, plus du kan vise det i en præsentation for at gøre dit punkt tydeligere.
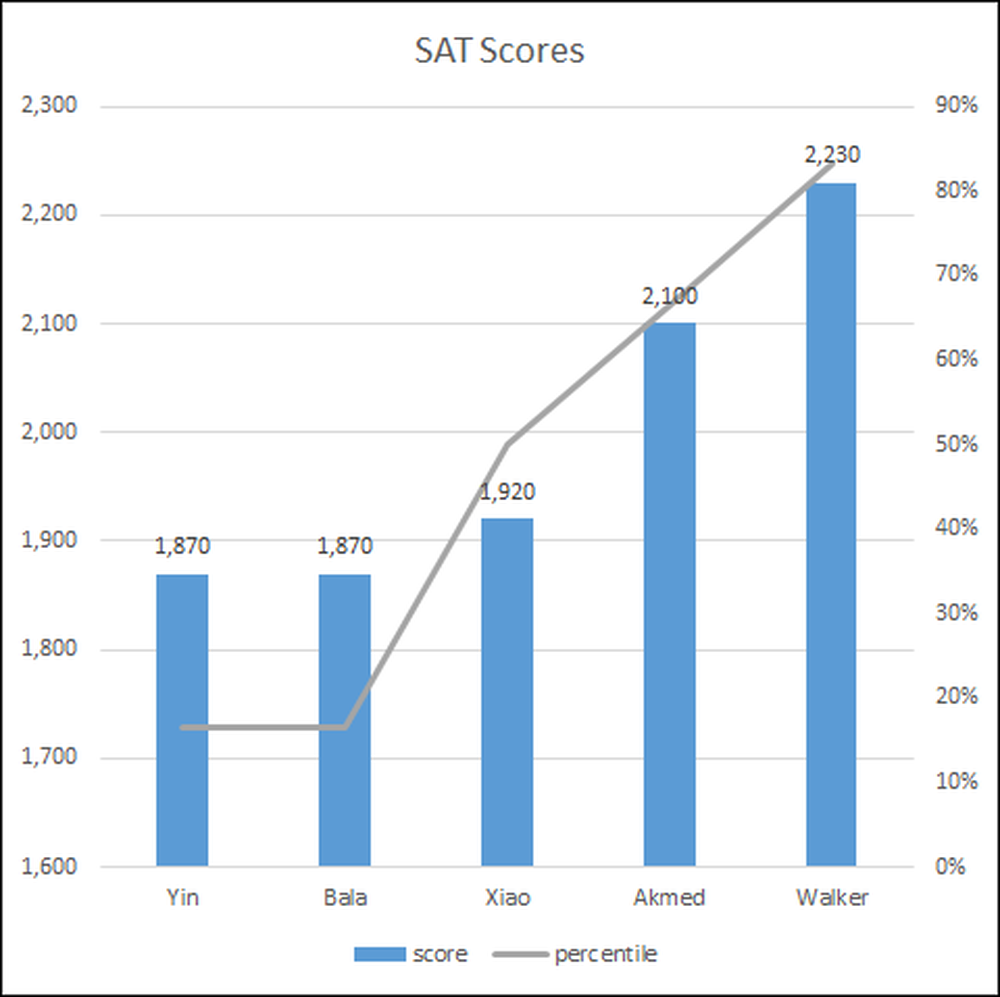
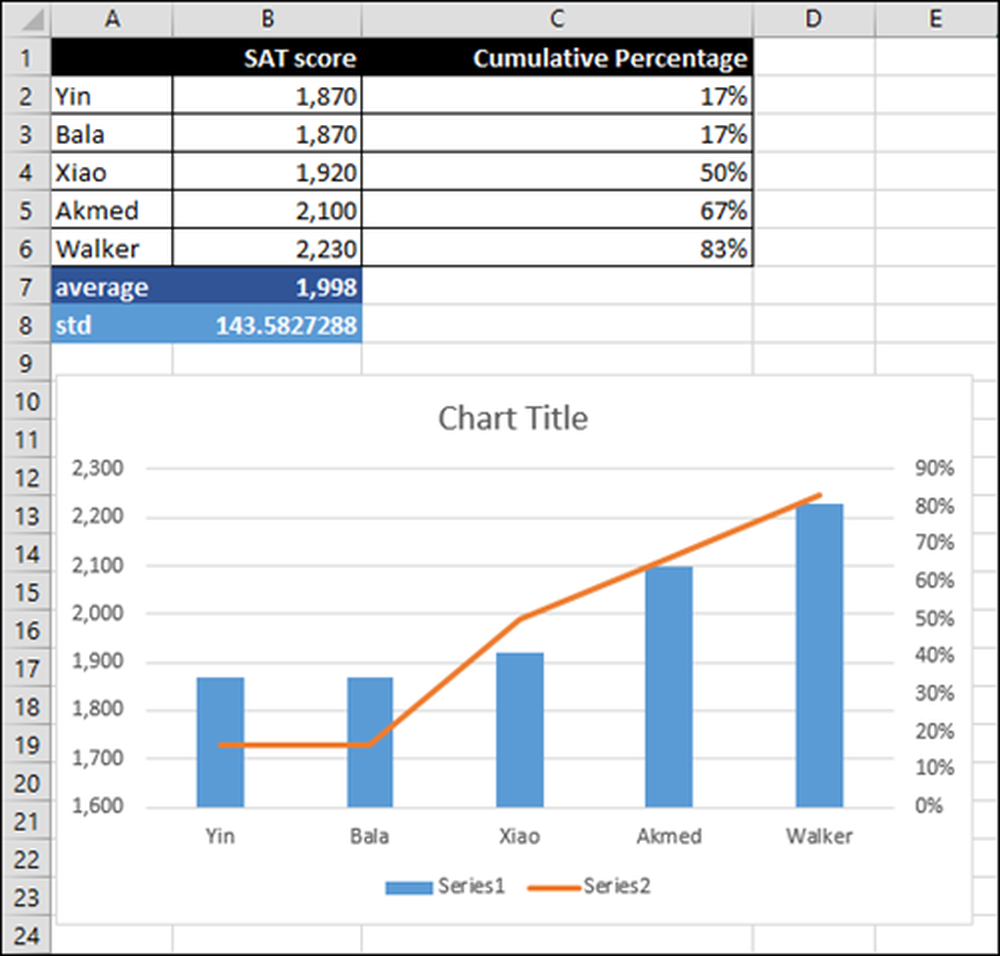
Studerende er på den vandrette akse, og deres SAT-scoringer vises som en blå søjlediagram på en skala (lodret akse) fra 1.600 til 2.300.
Den procentuelle rangering er den højre lodrette akse fra 0 til 90 procent og er repræsenteret af den grå linje.
Sådan opretter du et diagram
Oprettelse af et diagram er et emne for sig selv, men vi vil kortfattet forklare, hvordan ovenstående diagram blev oprettet.
Vælg først det område af celler, der skal findes i diagrammet. I dette tilfælde A2 til C6, fordi vi ønsker numrene såvel som den studerendes navne.
Fra menuen "Indsæt" vælg "Diagrammer" -> "Anbefalede diagrammer":

Computeren anbefaler en "Clustered-Column, Secondary Axis" diagram. Den "sekundære akse" del betyder at den trækker to vertikale akser. I dette tilfælde er dette diagram det, vi ønsker. Vi behøver ikke gøre noget andet.

Du kan bruge flytte diagrammet rundt og omforme det, indtil du har det som den størrelse og den ønskede position. Når du er tilfreds, kan du gemme diagrammet i regnearket.
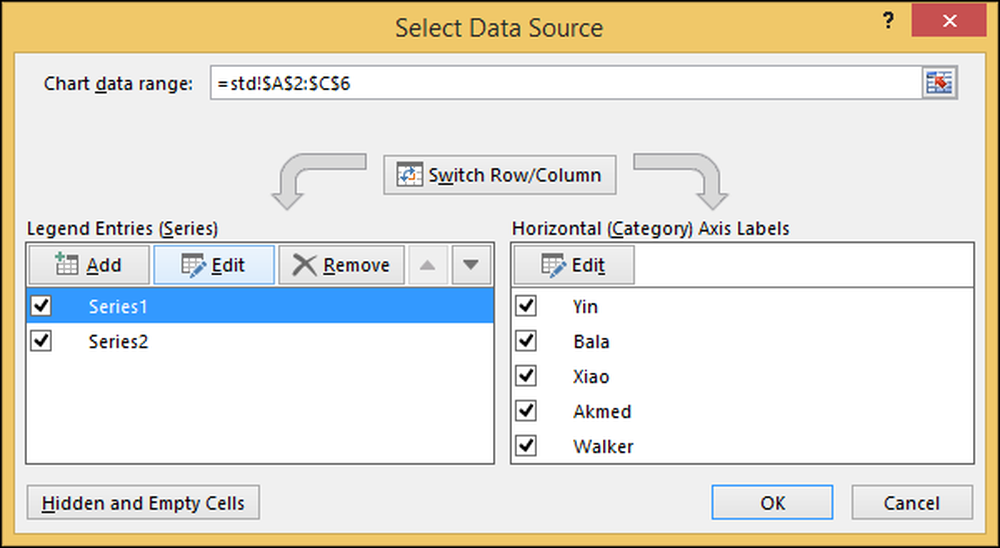
Hvis du højreklikker på diagrammet, vælger du "Vælg data", hvilke data der er valgt for området.
Funktionen "Anbefalede diagrammer" udfordrer dig normalt ud fra at skulle håndtere så komplicerede detaljer som at bestemme hvilke data der skal medtages, hvordan man tildeler etiketter og hvordan man tildeler venstre og højre lodrette akser.
I dialogboksen "Vælg datakilde" skal du klikke på "score" under "Legend Entries (Series)" og trykke "Rediger" og ændre det for at sige "Score."
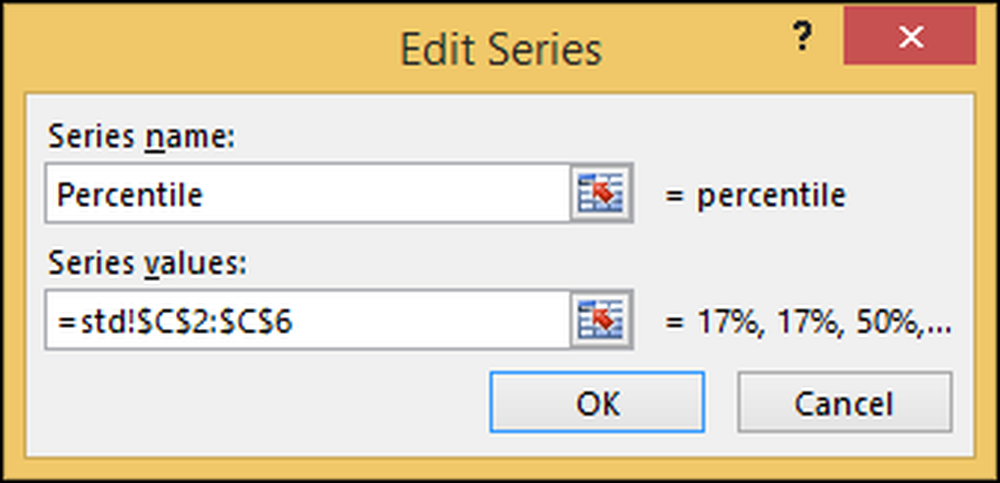
Derefter ændres serie 2 ("percentil") til "Percentile."
Gå tilbage til dit diagram og klik på "Chart Title" og skift det til "SAT Scores." Nu har vi et komplet diagram. Den har to vandrette akser: en til SAT-score (blå) og en for kumulativ procentdel (orange).

Eksempel: Transportproblemet
Transportproblemet er et klassisk eksempel på en type matematik kaldet "lineær programmering." Dette giver dig mulighed for at maksimere eller minimere en værdi emne for visse begrænsninger. Det har mange applikationer til bred vifte af forretningsproblemer, så det er nyttigt at lære, hvordan det virker.
Før vi begynder med dette eksempel, skal vi aktivere "Excel Solver".
Aktivér Solver Add-In
Vælg "File" -> "Options" -> "Add-ins". Nederst i tilføjelsesindstillingerne skal du klikke på knappen "Gå" ud for "Administrer: Excel-tilføjelser".
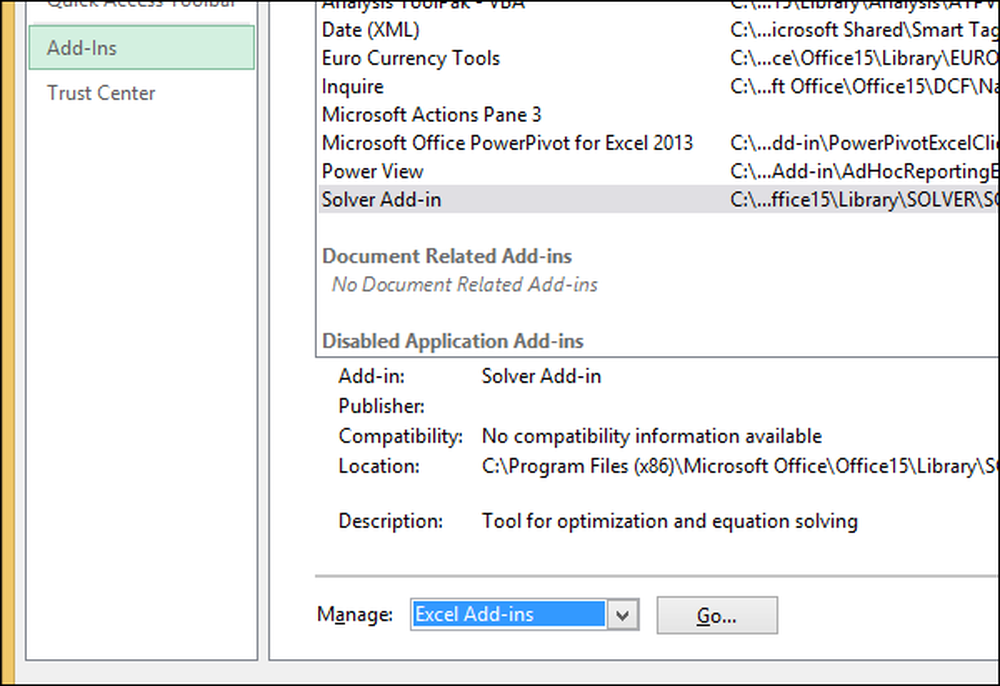
På den resulterende menu skal du klikke på afkrydsningsfeltet for at aktivere "Solver Add-in" og klikke på "OK".

Eksempel: Beregn de laveste iPad forsendelsesomkostninger
Antag, at vi leverer iPads, og vi forsøger at udfylde vores distributionscentre ved at bruge de laveste transportomkostninger. Vi har en aftale med et lastbil og flyselskab om at sende iPads fra Shanghai, Beijing og Hong Kong til distributionscentrene vist nedenfor.
Prisen, der sendes til hver iPad, er afstanden fra fabrikken til distributionscentret til fabrikken divideret med 20.000 kilometer. For eksempel er det 8.024 km fra Shanghai til Melbourne, som er 8.024 / 20.000 eller $ .40 per iPad.

Spørgsmålet er, hvordan sender vi alle disse iPads fra disse tre planter til disse fire destinationer til den lavest mulige pris?
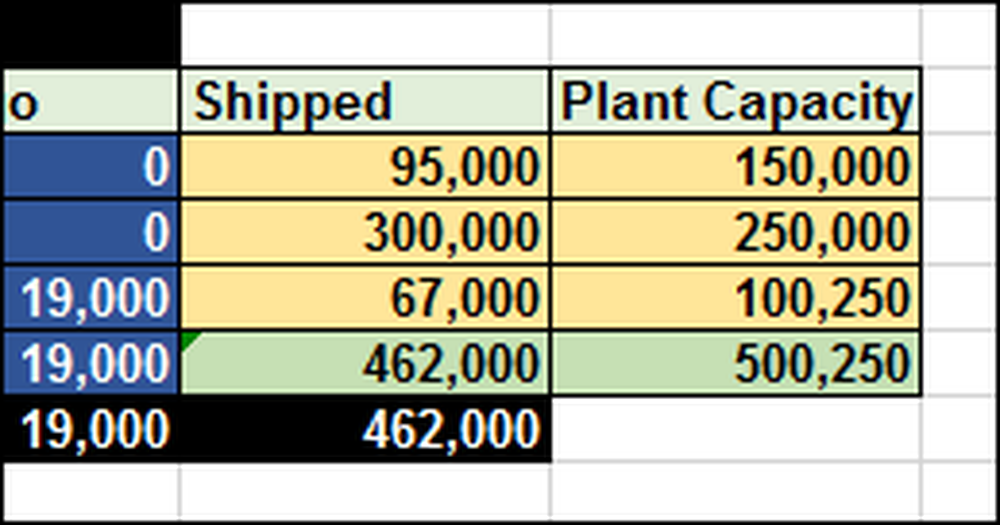
Som du kan forestille dig, kan det være meget svært at finde ud af det uden nogen formel og værktøj. I dette tilfælde skal vi sende 462.000 (F12) i alt iPads. Planterne har en begrænset kapacitet på 500.250 (G12) enheder.
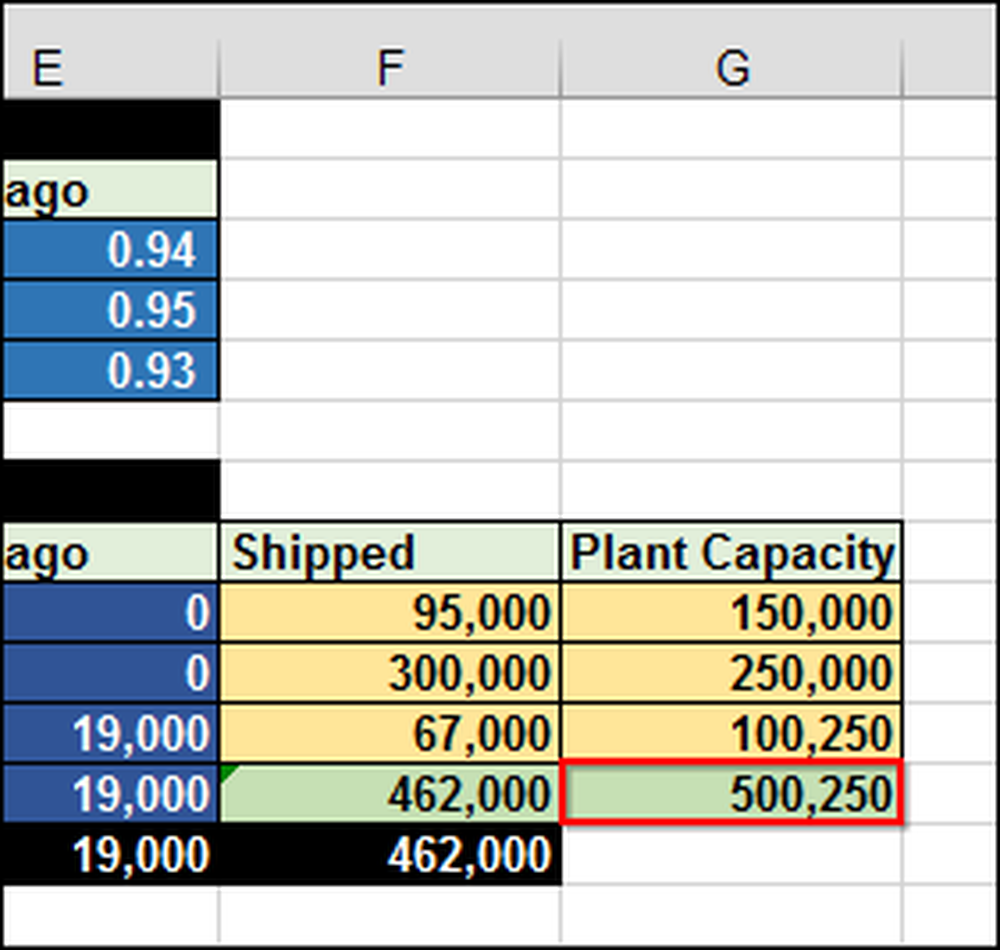
I regnearket, så du kan se, hvordan det virker, har vi skrevet 1 i celle B10, hvilket betyder, at vi ønsker at sende 1 iPad fra Shanghai til Melbourne. Da transportomkostninger langs den rute er $ 0,40 pr. IPad, er den samlede pris (B17) $ 0,40.

Nummeret blev beregnet ved hjælp af funktionen = SUMPRODUCT (omkostninger, afsendt) "omkostninger" er intervallerne B3: E5.
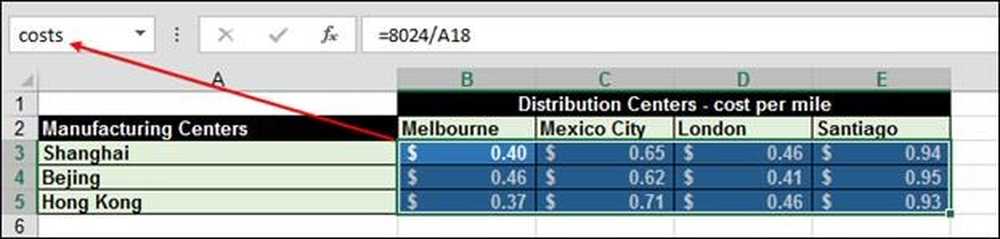
Og "afsendt" er området B9: E11:

SUMPRODUCT multiplicerer "omkostninger" gange rækkevidden "afsendt" (B14). Det kaldes "matrix multiplikation."
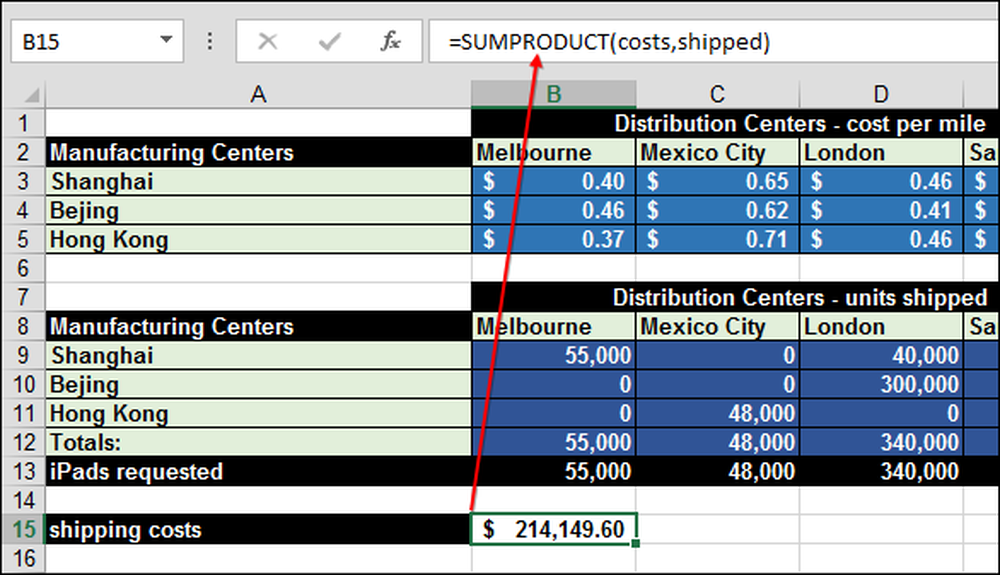
For at SUMPRODUCT skal fungere korrekt skal de to matricer - omkostninger og forsendelser - være lige store. Du kan omgå denne begrænsning ved at lave ekstra omkostninger og forsendelseskolonner og rækker med nulværdi, så arrayerne er af samme størrelse, og der er ingen indvirkning på de samlede omkostninger.
Brug af Solver
Hvis alt vi skulle gøre var at multiplicere matricerne "omkostninger" gange "afsendt", ville det ikke være for kompliceret, men vi skal også håndtere begrænsninger der.
Vi skal sende, hvad hvert distributionscenter kræver. Vi sætter det konstant ind i løsningen som denne: $ B $ 12: $ E $ 12> = $ B $ 13: $ E $ 13. Dette betyder summen af, hvad der sendes, dvs. summen i celler $ B $ 12: $ E $ 12, skal være større end eller lig med hvad hvert distributionscenter kræver ($ B $ 13: $ E $ 13).

Vi kan ikke sende mere end vi producerer. Vi skriver disse begrænsninger som denne: $ F $ 9: $ F $ 11 <= $G$9:$G$11. Put another way, what we ship from each plant $F$9:$F$11 cannot exceed (must be less than or equal to) the capacity of each plant: $G$9:$G$11.
Gå nu til "Data" menuen og tryk på "Solver" knappen. Hvis knappen "Solver" ikke er der, skal du aktivere Solver-tilføjelsen.
Indtast de to begrænsninger, der er detaljeret tidligere, og vælg "Forsendelser" -området, hvilket er antallet af tal, som vi ønsker at beregne Excel. Vælg også standard algoritmen "Simplex LP" og indikere at vi vil "minimere" cellen B15 ("samlede forsendelsesomkostninger"), hvor der står "Set Objective."
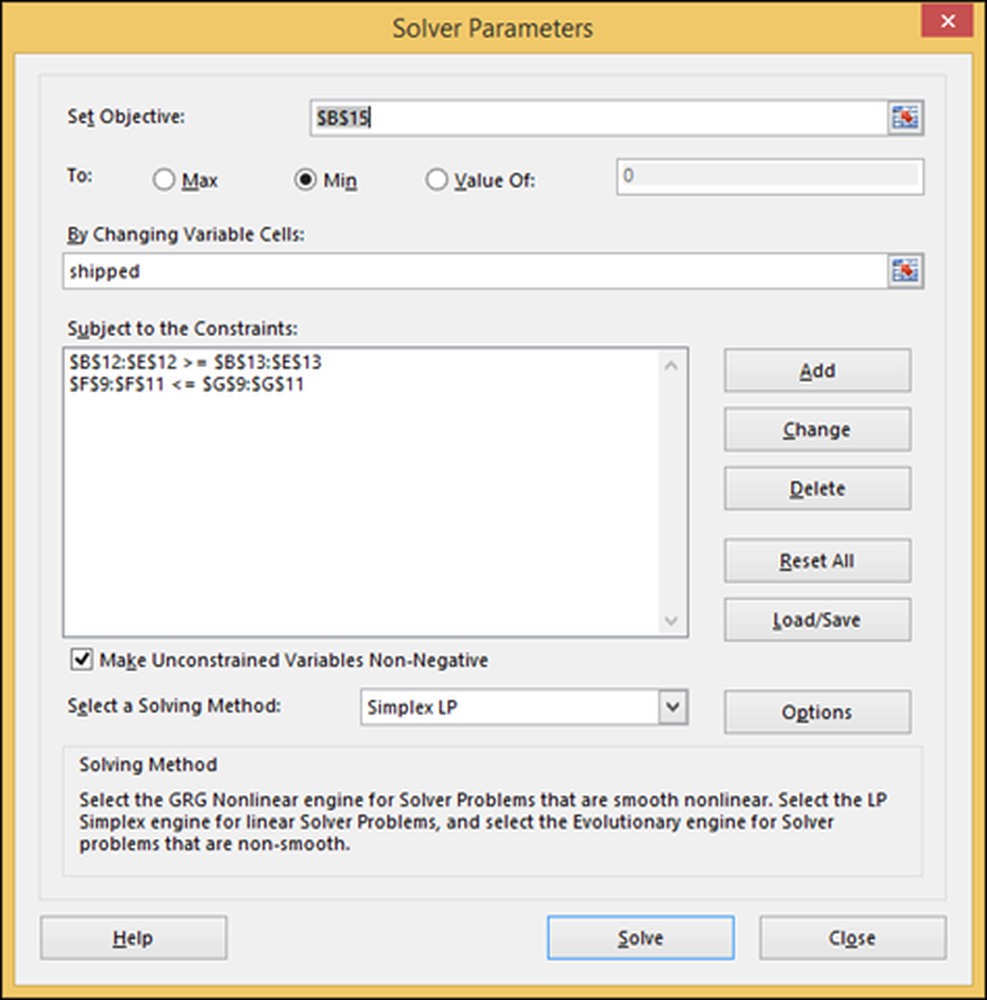
Tryk på "Løs" og Excel gemmer resultaterne i regnearket, hvilket er det, vi ønsker. Du kan også gemme dette, så du kan lege med andre scenarier.
Hvis computeren siger, at den ikke kan finde en løsning, har du gjort noget, der ikke er logisk, for eksempel har du måske bedt om flere iPads end planterne kan producere.
Her siger Excel, at den har fundet en løsning. Tryk på "OK" for at holde løsningen og vende tilbage til regnearket.
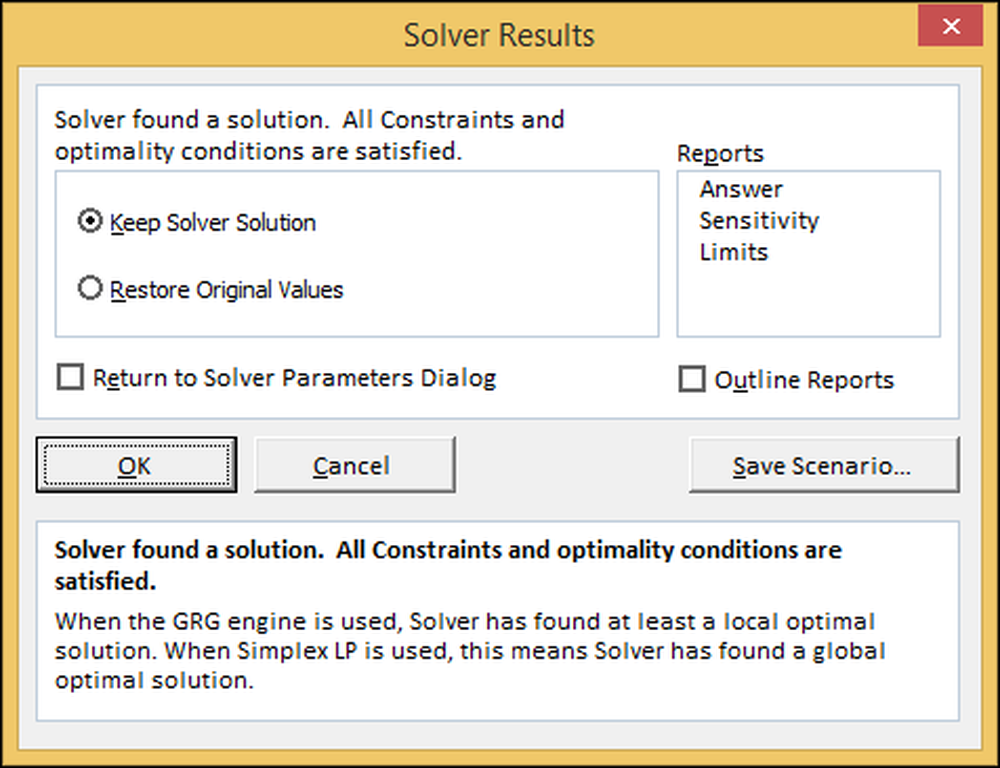
Eksempel: Netto nutidsværdi
Hvordan beslutter et firma om at investere i et nyt projekt? Hvis "Netto nutidsværdi" (NPV) er positiv, vil de investere i det. Dette er en standard fremgangsmåde taget af de fleste finansielle analytikere.
Antag for eksempel, at Codelco-mineselskabet ønsker at udvide Andinas kobbermine. Standardmetoden til at bestemme, om man skal fortsætte med et projekt, er at beregne nutidsværdien. Hvis NPV er større end nul, vil projektet være rentabelt med to inputs (1) tid og (2) kapitalomkostninger.
I almindelig engelsk betyder kapitalomkostninger, hvor meget de penge ville tjene, hvis de netop forlod det i banken. Du bruger kapitalkostnaden til at diskontere kontante værdier til nutidsværdi, med andre ord $ 100 om fem år kan være $ 80 i dag.
I det første år er 45 millioner dollars afsat som kapital til finansiering af projektet. Revisorerne har fastslået, at deres kapitalomkostninger er seks procent.

Da de begynder minedrift, begynder kontanterne at komme ind, da firmaet finder og sælger det kobber, de producerer. Det er klart, jo mere de mine, jo flere penge de laver, og deres prognose viser, at deres pengestrømme stiger, indtil det når op til 9 millioner dollars om året.
Efter 13 år er NPV $ 3.945.074 USD, så projektet vil være rentabelt. Ifølge finansanalytiker er "tilbagebetalingstid" 13 år.
Oprettelse af en pivottabel
Et "drejebord" er dybest set en rapport. Vi kalder dem pivottabeller, fordi du nemt kan skifte dem en type rapport til en anden uden at skulle lave en helt ny rapport. Så de omdrejningspunkt på plads. Lad os vise et grundlæggende eksempel, der lærer de grundlæggende begreber.
Eksempel: Salgsrapporter
Salgsfolk er meget konkurrencedygtige (det er en del af at være en sælger), så de vil naturligvis vide, hvordan de går imod hinanden i slutningen af kvartalet og i slutningen af året, plus hvor meget deres provisioner vil blive.
Antag, at vi har tre salgsfolk - Carlos, Fred og Julie - alle sælger olie. Deres salg i dollar pr. Regnskabsår for 2014 er vist i regnearket nedenfor.
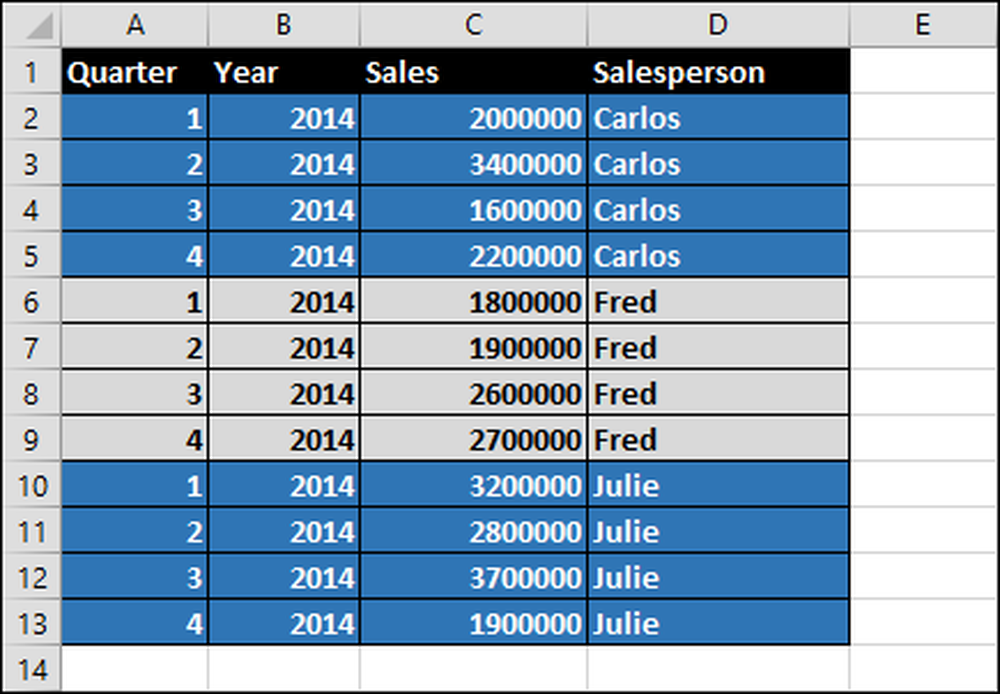
For at generere disse rapporter opretter vi en pivottabel:
Vælg "Insert -> Pivot Table, den er på venstre side af værktøjslinjen:
Vælg alle rækker og kolonner (herunder sælgerens navn) som vist nedenfor:
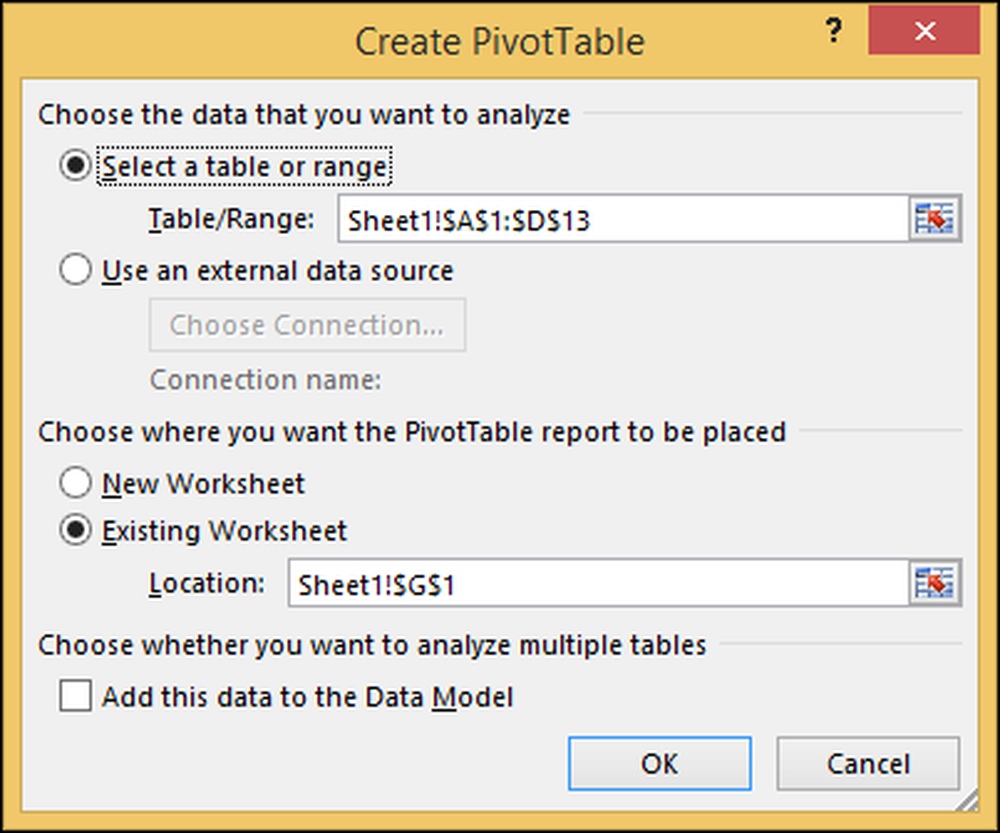
Dialogboksen for drejebordet vises til højre for regnearket.
Hvis vi klikker på alle fire felter i pivottabellens dialogboks (kvartal, år, salg og sælger) tilføjer Excel en rapport til regnearket, der ikke giver mening, men hvorfor?
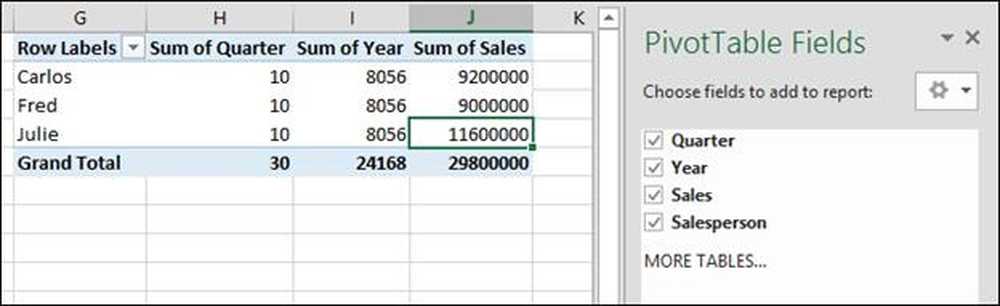
Som du kan se, har vi valgt alle fire felter, der skal tilføjes til rapporten. Excel's standardadfærd er at gruppere rækker ved hjælp af tekstfelter og summen derefter hele resten af rækkerne.
Her giver det os summen af 2014 + 2014 + 2014 + 2014 = 24.168, hvilket er nonsens. Det gav også summen af kvartalerne 1 + 2 + 3 + 4 = 10 * 3 = 3 0. Vi har ikke brug for disse oplysninger, så vi afmarkerer disse felter for at fjerne dem fra vores drejebord.
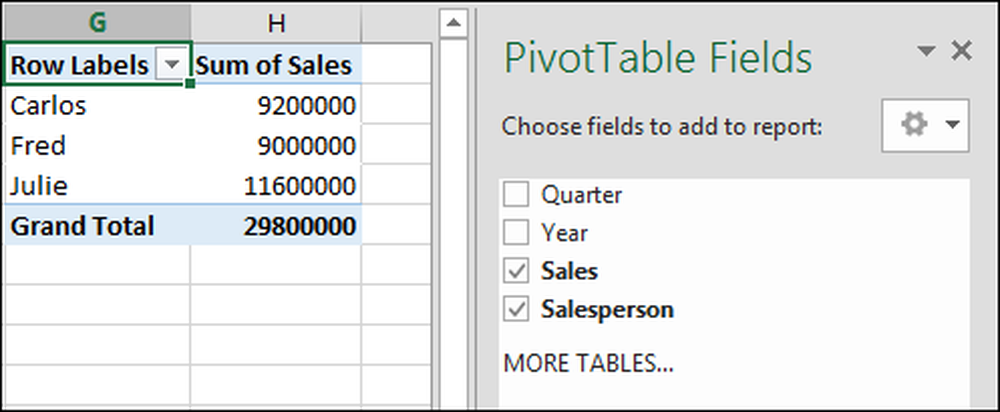
Summen af salg (samlet salg) er imidlertid relevant, så vi vil rette det.
Eksempel: Salg af sælger
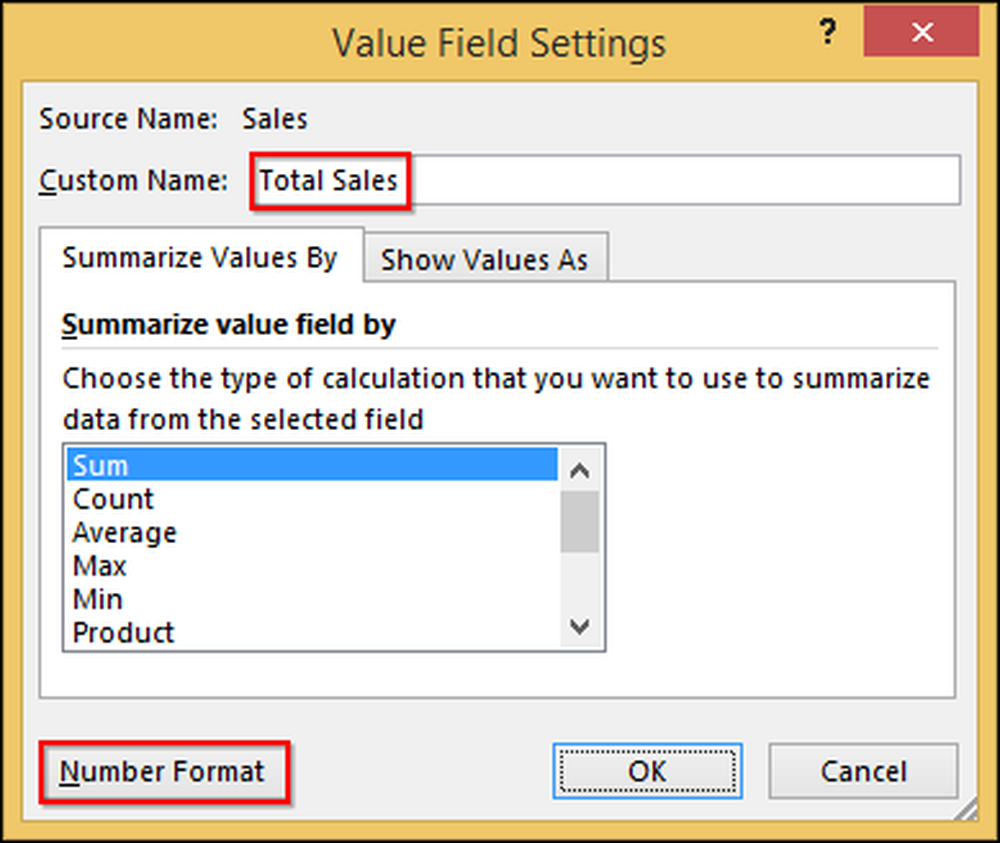
Du kan redigere "Sum of Sales", der siger "Total Sales", hvilket er tydeligere. Du kan også formatere cellerne som valuta ligesom du ville formatere andre celler. Klik først på "Sum of Sales" og vælg "Value Field Settings."

I den resulterende dialog ændrer vi navnet til "Total salg" og klik derefter på "Nummerformat" og ændrer det til "Valuta".
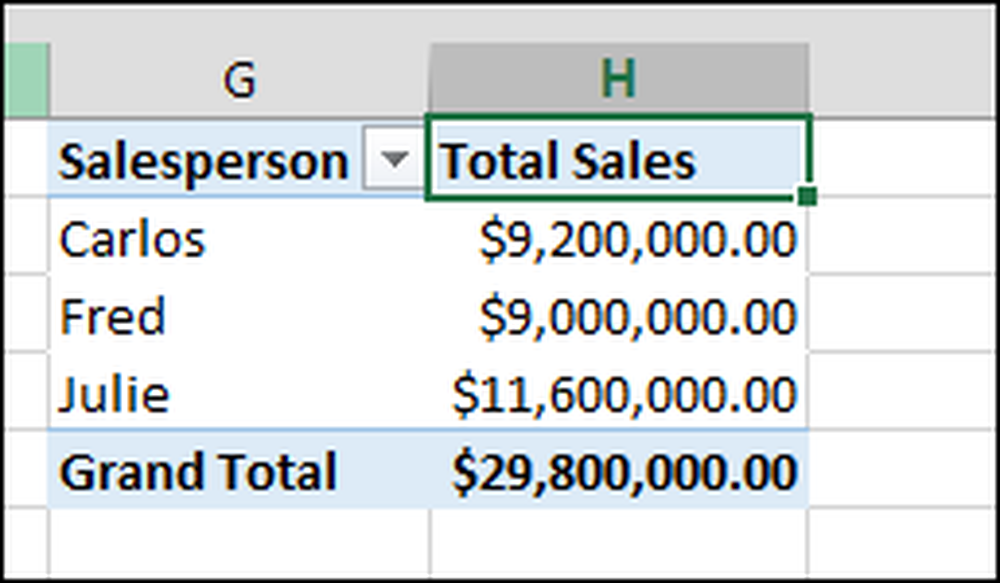
Du kan så se dit håndarbejde i pivottabellen:
Eksempel: Salg af sælger og kvartal
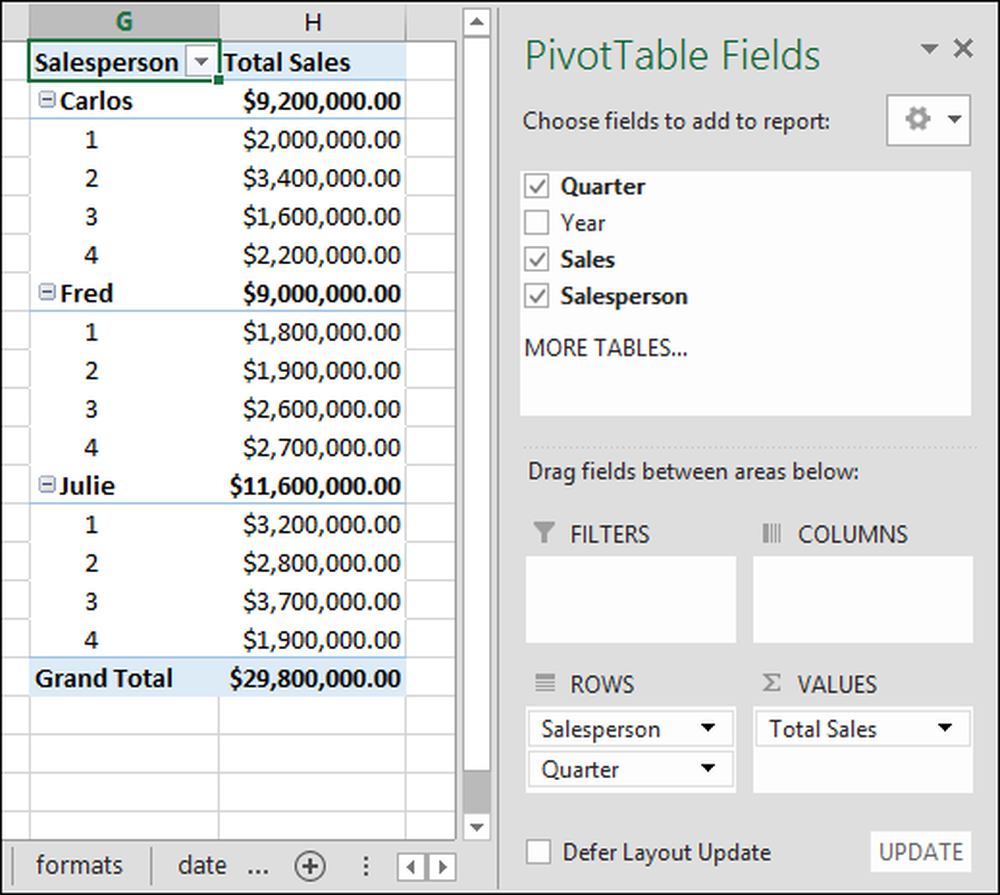
Lad os nu tilføje subtotaler for hvert kvartal. For at tilføje subtotaler skal du blot venstreklikke på feltet "Kvartal" og holde og træk det til "rækker" sektionen. Du kan se resultatet på skærmbilledet nedenfor:

Mens vi er i det, lad os fjerne værdien "Sum of Quarter". Du skal blot klikke på pilen og klikke på "Fjern felt". I skærmbilledet kan du nu se, at vi har tilføjet "Quarter" rækkerne, der nedbryder hver sælgers salg pr. Kvartal.
Med disse færdigheder ny i tankerne kan du nu oprette pivottabeller fra dine egne data!
Konklusion
Indpakning, vi har vist dig nogle af funktionerne i Microsoft Excel's formler og funktioner, som du kan anvende Microsoft Excel til din virksomhed, akademiske eller andre behov.
Som du har set, er Microsoft Excel et enormt produkt med så mange funktioner, at de fleste mennesker, endda avancerede brugere, ikke kender dem alle. Nogle mennesker kan sige, at det gør det kompliceret; vi føler det mere omfattende.
Forhåbentlig har vi ved at præsentere dig mange eksempler på virkelige eksempler vist ikke kun de funktioner, der er tilgængelige i Microsoft Excel, men har lært dig noget om statistik, lineær programmering, oprettelse af diagrammer, brug af tilfældige tal og andre ideer, som du nu kan vedtage og brug i din skole eller hvor du arbejder.
Husk, hvis du vil gå tilbage og tage klassen igen, kan du begynde at friske med lektion 1!




